Determinanty - Príklad 5

Determinanty

Príklad 5

Riešte nasledujúcu nerovnicu:
$$
\left|
\begin{array}{lrr}
x^2& 4& 9\\
x& 2& 3\\
1 &1& 1\\
\end{array} \right|>0
$$

Riešenie:

V prvom rade je potrebné vypočítať determinant:

$$
\left|
\begin{array}{lrr}
x^2& 4& 9\\
x& 2& 3\\
1 &1& 1\\
\end{array} \right|=2x^2+9x+12-(18+3x^2+4x)=-x^2+5x-6>0
$$

Po výpočte determinantu sa úloha pretransformovala na úlohu:
Riešte kvadratickú nerovnicu:
$$
-x^2+5x-6>0
$$

Na riešenie tejto nerovnice je možné použiť viacero metód. Uvedieme dve základné:

• I. Metóda nulových bodov,
• II. grafické riešenie.

I. Metóda nulových bodov:
\begin{eqnarray*}
-x^2+5x-6&>&0\\
x^2-5x+6&<&0
\end{eqnarray*}
Nulovým bodom výrazu budeme nazývať také číslo, v ktorom výraz $x^2-5x+6=0$ nadobúda hodnotu nula.
Výraz  $x^2-5x+6=0$ je možné napísať v tvare súčinu, podľa nasledujúceho vzťahu:
$$ax^2+bx+c=a(x-x_1)(x-x_2),$$ kde $x_1$ a $x_2$ sú korene kvadratickej rovnice  $ax^2+bx+c=0$.
Korene kvadratickej rovnice môžeme vypočítať napr. podľa vzťahu:
$$x_{1,2}=\frac{-b\stackrel{+}{-} \sqrt{b^2-4ac}}{2a} $$
V našom prípade $x^2-5x+6=(x-3)(x-2)$.

Vidíme, že jeden zo súčiniteľov môže zmeniť znamienko iba v čísle $3$ a druhý súčiniteľ iba v čísle $2$. Tieto dve čísla rozdeľujú množinu reálnych čísel na tri podintervaly $(-\infty, 2), (2, 3\rangle, \langle 3, \infty)$, v ktorých vyšetríme znamienko súčinu.

V intervale $\left(-\infty; 2\right)$ je prvý aj druhý činiteľ záporný. Výsledný súčin je na tomto intervale kladný.
V intervale $\left(2; 3\right)$ je prvý činiteľ kladný a druhý záporný. Výsledný súčin nadobúda na tomto intervale zápornú hodnotu.
V intervale $\left(3;\infty\right)$ je prvý aj druhý činiteľ kladný. Výsledný súčin je na tomto intervale kladný.

Súčin bude záporný, ak $x$ bude patriť do intervalu: $\left(2;3\right)$.

Riešením tejto nerovnice je teda množina reálnych čísel $\left(2;3\right)$.

II. Grafické riešenie
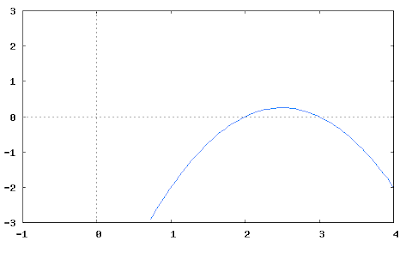
Grafom funkcie $y=-x^2+5x-6$ je parabola. V prvom rade nás zaujímajú priesečníky s osou $x$. Všeobecne takýto priesečník má súradnice $P_x=[x;0]$. Priesečník zistíme tak, že do predpisu funkcie za $y$ dosadíme $0$ a $x$ ponecháme. Takouto úpravou získame kvadratickú rovnicu:
$$ -x^2+5x-6 = 0$$
V našom prípade má kvadratická rovnica dva reálne korene: $2$ a $3$.
Parabola, ktorá je grafom tejto funkcie pretína os $x$ práve v týchto dvoch číslach. Keďže koeficient pri $x^2$ je $-1$ t.j záporné číslo, bude mať parabola konkávny tvar.

Našou úlohou je riešiť kvadratickú nerovnicu: $- x^2+5x-6 > 0$. Hodnoty funkcie (tie odčítavame na osi $y$) majú byť menšie ako nula. To nastane, ako je vidieť z grafu, keď $ x\in(2;3) $.
Keďže  $y>0$, tak riešením je interval $\left(2;3\right)$.